Planimetria

• Miary kątów w trójkącie

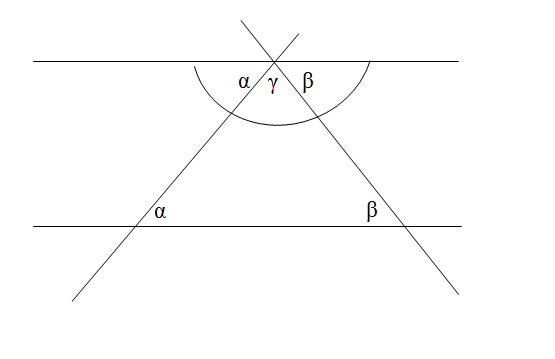
• Rozpatrzymy trójkąt ABC (rysunek obok). Rysujemy pomocniczą prostą l równoległą do boku AB, przechodzącą przez wierzchołek C. Kąty ɑ i ɑ' są równe (są to kąty naprzemmianległe). Również kąty β i β' są równe (jako kąty naprzemianległe). Zatem ɑ + β + γ = ɑ' + β' + γ. ɑ' + β' + γ = 180° ,więc również: ɑ + β + γ = 180°

• Udowodniliśmy w ten sposób ,że suma miar kątów wewnętrznych w dowolnym trójkącie jest równa 180°.

• Uwaga. Tam, gdzie nie powoduje to nieporozumień ,będziemy zamiennie używać określeń "kąt" i "miara kąta".



• Trójkąty przystające

  Cecha BBB

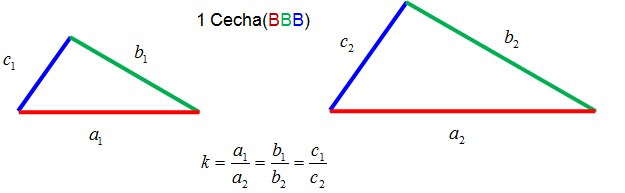
• Jeśli trzy boki jednego trójkąta są odpowiednio równe trzem bokom drugiego trójkąta, to trójkąty te są przystające.

• Jeśli a = a', b = b' i c = c' to trójkąty ABC i A'B'C' są przystające ,co zapisujemy:

• ΔABC ≡ ΔA'B'C'



Cecha BKB

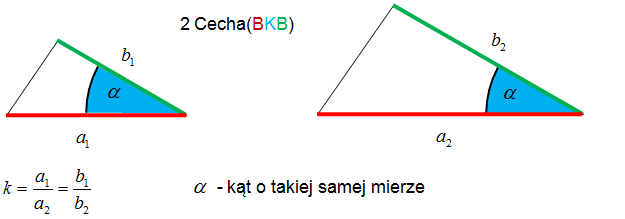
• Jeśli dwa boki i kąt zawarty między nimi w jednym trójkącie są odpowiednio równe dwóm bokom i kątowi zawartemu między nimi w drugim trójkącie, to trójkaty te są przystakące.

• Jeśli a = a' ,b = b' i γ = γ',to:

• ΔABC ≡ ΔA'B'C'



Cecha KBK

• Jeśli bok i dwa leżące przy nim kąty w jednym trójkącie są odpowiednio równe bokowi i dwóm leżącym przy nim kątom w drugim trójkącie, to trójkąty te są przystające.

• Jeśli b = b' ,α = α' i γ = γ',to:

• ΔABC ≡ ΔA'B'C'



• Twierdzenie Talesa

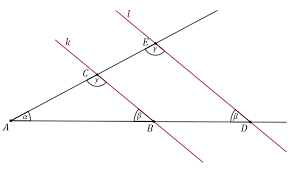
• Jeżeli ramiona kąta AOA' są przecięte dwiema prostymi równoległymi
  AA' i BB'
  ,to długości odcinków wyznaczonych przez te proste na jednym ramieniu tego kąta są proporcjonalne do długości odpowiednich odcinkówwyznaczonych przez te proste na drugim ramieniu:

• |OA'|/|OA|
  =
  |A'B'|/|AB|
  oraz
  |OA'|/|OA|
  =
  |OB'|/|OB|



Darmowy hosting zapewnia PRV.PL