Funkcja kwadratowa
-
Wykres funkcji f(x) = ax²
- Na rysunku poniżej przedstawiono parabolę ,która jest wykresem funkcji f(x) = x². Jej dziedziną jest zbiór liczb rzeczywistych ,a zbiorem wartości - przedział ‹0;∞›. Z wykresu możemy odczytać następujące własności:
- a) ramiona paraboli są skierowane do góry
- b) oś 0Y jest osią symetrii paraboli
- c) punkt (0,0) jest wierzchołkiem paraboli
- d) funkcja f jest malejąca w przedziale (-∞;0› i rosnąca w przedziale ‹0;∞)
- e) dla x = 0 funkcja f przyjmuje wartość najmniejszą równą zeru, natomiast dla każdego x ≠ 0 prawdziwa jest nierówność f(x) > 0
- f) funkcja f nie przyjmuje wartości największej

-
Przesunięcie wykresu funkcji f(x)= ax² o wektor
- Przykład 1
- Wykres funkcji f(x) = 2x² - 4 otrzymamy, przesuwając parabole y = 2x² o 4 jednostki w dół ,czyli o wektor u = [0,-4]

- Przykład 2
- Wykres funkcji f(x) = 2(x-3)² otrzymamy, przesuwając parabole y = 2x² o 3 jednostki w prawo, czyli o wektor u = [3,0] (rysunek obok)
- Przykład 3
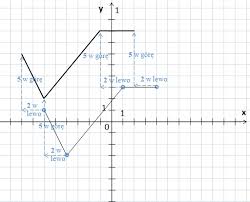
- Wykres funkcji f(x) = (x-2)²+1 otrzymamy przesuwając parabole y = x² o 2 jednostki w prawo ,a następnie o 1 jednostkę w górę, lub bezpośrednio o wektor u = [2,1].
-
Postać kanoniczna i postać ogólna funkcji kwadratowej
- Definicja
- Postać: y = ax² + bx + c, gdzie a,b,c należą do R, a ≠ 0 nazywamy postacią ogólną funkcji kwadratowej.
- Postać: y = a(x - p)² + q, gdzie a,p,q należą do R, a ≠ 0 nazywamy postacią kanoniczną funkcji kwadratowej.
-
Odnośniki